
기존의 개인키의 문제점과 공개키에 대한 내용 그리고 대표적인 공개키인 RSA에 대해 알아봅시다
공개키를 모르는 상황이라면 암호화에 쓰일 수 있는 것은 대칭키일 것이다.
이 대칭키에서의 문제점은 대칭 키의 분배에 있다.
만약 그 대칭키가 유출된다면 암/복호화는 식은죽 먹기가 된다.
그래서 해당 키를 어떻게 분배해야 하는지도 중요해진다.

공개키는 단어 뜻 그자체로 키를 공개한다? 라는 의미로 받아들여진다.
하지만 원리는 두개의 키가 존재하는 것이다.
그것은 공개키 & 비밀키로 서로 비대칭적이다. 즉 다른 것이라는 뜻이다.
이러한 공개키 비밀키의 메커니즘은 Hard problem을 기반으로 해서 만들어진다.
p, np문제.. 뭐 이런 내용들은 기억이 가물가물하지만 어쨌든 풀기가 상당히 어려운 문제라는 것이다.
어쨌든 이런 공개키 메커니즘은 대칭키와 다르게 기능은 좋지만 느리다는 장점이 있다.

쓰일 수 있는 곳은 크게 두 가지로 분류해 볼 수 있다.
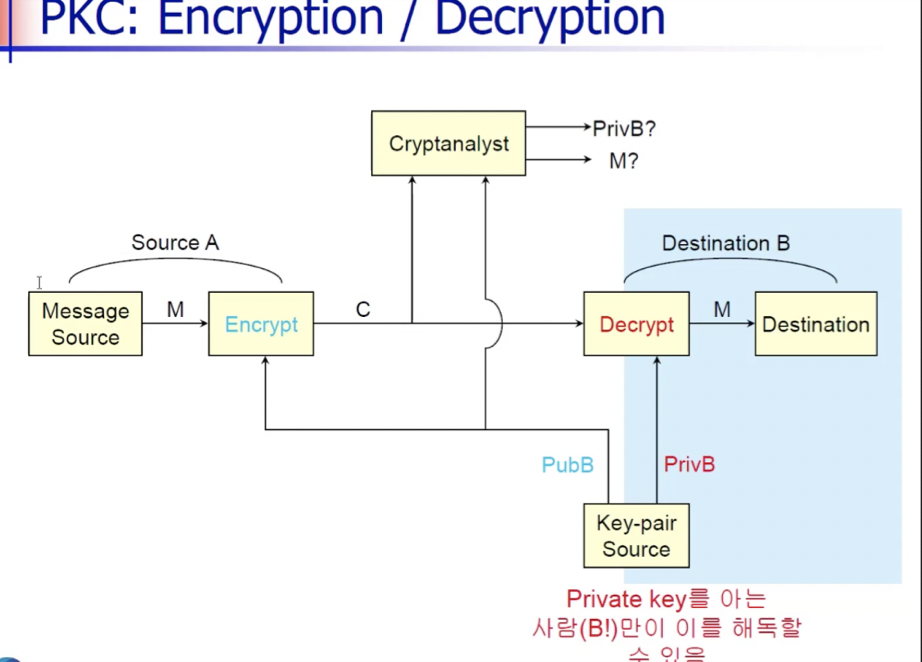
하나는 메시지의 암/복호화
: 암호화(수신자의 공개키) 복호화(수신자의 개인키)
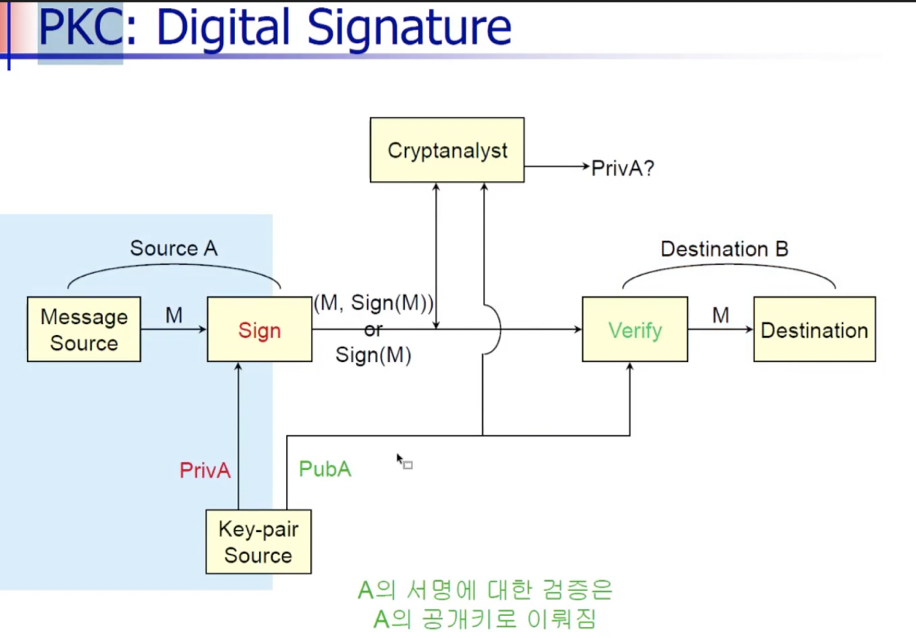
두 번째는 서명의 생성과 검증이다.
: 서명(송신자의 개인키) 검증( 송신자의 공개키)
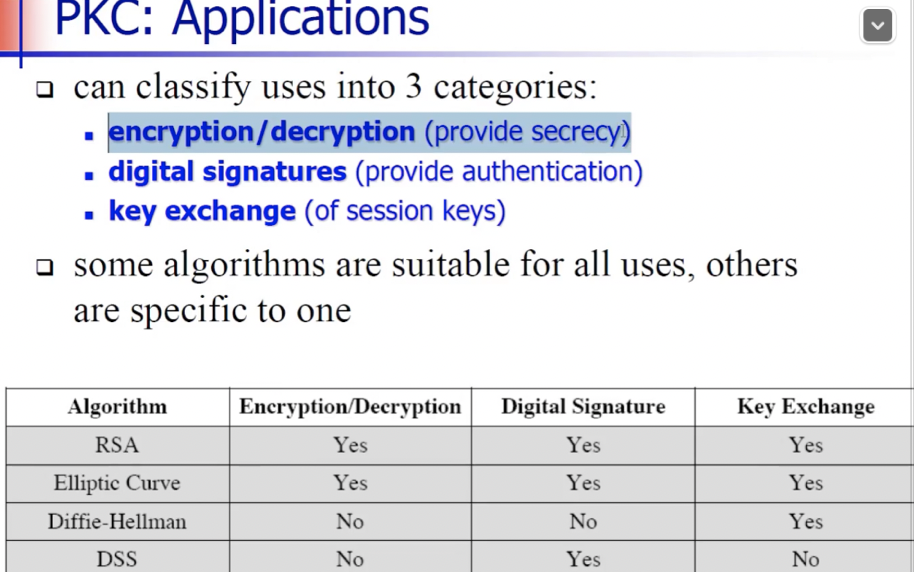
RSA, EC, DH, DSS와 같은 공개키 알고리즘을 쓸 수 있으며 각 알고리즘이 사용될 수 있는 용도가 있다.
dss는 서명만을 위한 알고리즘이다.

이런 PKC 즉, 공개키 시스템에서 요구되어지는 것은 다음과 같다.
복호화 키를 찾는 것이 힘들어야 하고
키를 알고 있을 때 계산하기 쉬워야 한다.
그리고 두 개의 키가 존재할 때, 하나는 암호화 하나는 복호화로 사용되어야 한다.
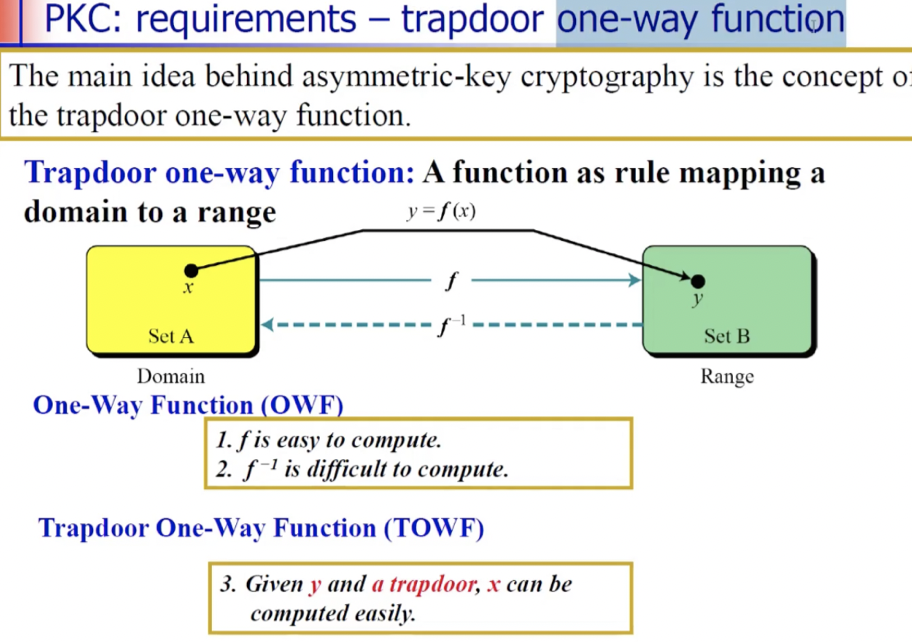
이러한 공개키 시스템은 trapdoor one-way function이라고 부른다.
one-way function이라면 해시 함수를 뜻한다.
trapdoor가 붙음으로써 이 trapdoor정보가 있으면 y에서 x로도 갈 수 있다는 것이다.

예를 보자.
ex1>
p와 q가 prime number이다. p*q는 쉽지만 n을 줘도 p와 q를 구하는 건 어렵다
= 소인수 분해의 어려움
But p나 q를 알면 쉽겟지 그니까 트랩도어 one way이다
ex2>
X, k, n을 y 구하기 y, k, n ᄌ면 어렵다
=> 이산 대수의 어려움
K”을 알고 있다 이건 k의 역원 , 이때 구할수 있다 , 이때 파이오브 n 공간인데.
파이 오브자체를 구하는게 어렵다 소수면 쉬웠지만 어렵다
양변에 k”승 곱해줘서 y = xmodn이 됨

이런 공개키 시스템의 안정성은 어떠한가?
이 hard problem을 hacking 한다 그리고 무식한 관점에서 brute force로 해결하려고 한다면 이는 infeasible 하다
하지만 부채널 공격이나, AI를 이용한 공격 방법들이 최근에 나오고 있는 것으로 알고 있다.

대표적인 공개키 암호인 RSA에 대해 보자.
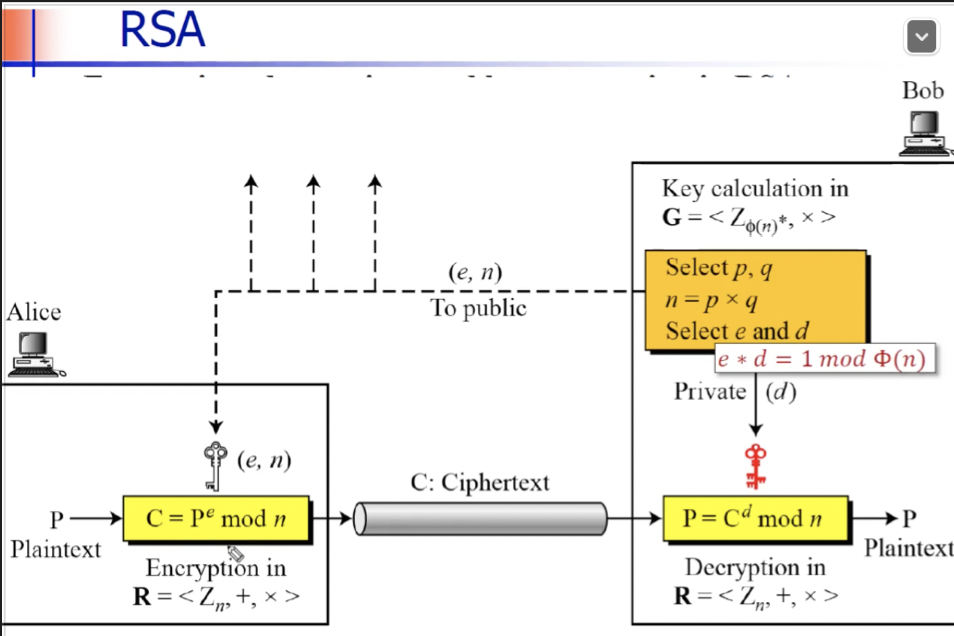
원리는 이 사진 하나로 끝이 난다.
참고로 이산수학에 대한 베이스가 없다면 이해하기 힘들 수도 있다.
여기에 이산수학에 대한 부분은 따로 정리를 하지 않았다.
기본적으로 평문을 암호화를 할 것이다.
bob의 공개키로 alice가 암호화를 한다고 치자.
bob은 p와 q를 구한다. 이 p와 q는 엄청 큰 소수이다.
그리고 p와 q를 곱해 n을 만든다. 만약 이 n을 알게 된다 해도 p와 q를 알아내기 상당히 힘들다. 한번 해보시길
그리고 큰 소수 p와 q를 곱해 더 커진 n에 대해서 파이 오브 n을 구한다.
파이 오브 n은 n-1까지의 수들을 나열해 n과 서로소인 것의 개수이다.
만약 파이 오브 n에서 n이 소수이면 이는 n-1이 된다. 예를 들면 5인 경우 파이오브 5는 4가 되는것이다.
만약 n을 안다고 해도 파이 오브 n을 쉽게 구할수 있을까 ? 상당히 어렵다
하지만 p와 q를 안다면 파이 오브 p와 파이 오브 q를 곱해서 파이오브 n이 나온다.
그런데 위에서 소수이면 파이오브 n이 n-1이라고 했고 이는 엄청 간편하다. 그리고 p와 q는 소수다.
그럼 간단하게 곱셈 한 번에 나와버린다.
하지만 이 p와 q를 곱한 n을 본 입장에서는 파이오브 n을 구하기가 상당히 어렵다.
이 mod 파이 오브 n공간에서 임의의 d에 대한 역원을 구하고 그것이 e가 된다.
그렇게 공개키 (e, n) 이 완성이 된다.
alice는 평문에 e승을 하고 mod n을 해서 보낸다.
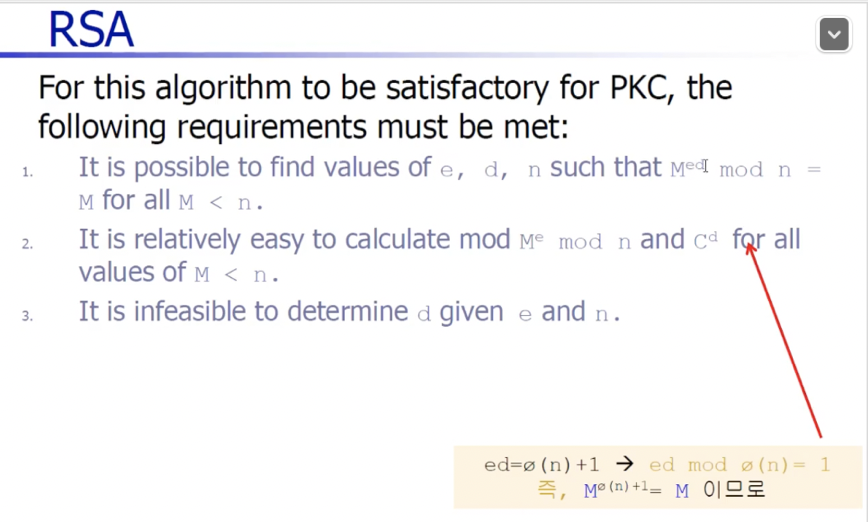
그리고 bob은 오른쪽 밑에 있는 정리를 사용하는데 이것은 오일러의 정리이다.
결국은 간단하게 평문만 남게 된다.

이 예제를 통해 좀 더 쉽게 이해해보자.
이러한 RSA의 계산을 쉽게 하기 위한 exponential 방법이나 decryption 방법들도 존재한다.
그것에는 CRT 같은 방법이 쓰일 수 있다.
'Infomation_Security' 카테고리의 다른 글
| 메세지 인증(MAC)과 해시 함수 (0) | 2021.08.20 |
|---|---|
| 공개키 키 관리기법 (0) | 2021.08.19 |
| AES (0) | 2021.08.07 |
| Block Cipher mode (0) | 2021.07.17 |
| Block Cipher(블록 암호화) (0) | 2021.07.17 |